The Embodied Perspective
I am a Strange Loop
A strange loop can be seen as a form of recursion that creates a sense of infinity.*Douglas R. Hofstadter, Gödel, Escher, Bach; Douglas R. Hofstadter, I Am a Strange Loop (Basic Books, 2007). The term recursion here is important. It originates in computer sciences and consists of a programming technique where a function calls itself to solve a problem. In addition, this concept has been adopted to describe elements that appear repeated in self-similar ways. For example, in nature, recursive structures are found in crystals and plants.*Benoit B. Mandelbrot, The Fractal Geometry of Nature, Updated and Augmented ed. (New York: Freeman, 1983).
In music, the concepts of recursion and self-similarity have given rise to vast investigations and the development of diverse compositional applications for them. Even though there are many approaches to music composition using these notions, most authors relate this idea to techniques of counterpoint. In particular, those that have their origin in the prolatio canon, which depends mainly on the simultaneous rendition of the same theme at various temporal scales. Early examples of these techniques can be found in works by the Renaissance composer Johannes Ockeghem and more recurrently in the music of Josquin Des Prez. A contemporary composer who made extensive use of prolatio techniques in his composition is Conlon Nancarrow.*See for example Kyle Gann, The Music of Conlon Nancarrow, vol. 7 (Cambridge University Press, 1995).
Another counterpuntual technique that has been associated with the idea of recursion and self-similarity is the crab canon. A crab canon or canon cancricans results when a cantus firmus is used in its backward form –retrograde– as a counterpoint of itself in original form.*H. Riemann and S.H. Lovewell, Text-book of Simple and Double Counterpoint Including Imitation Or Canon (Breitkopf & Härtel, 1904). Johann Sebastian Bach makes use of this resource recurrently in his Musical Offering, BWV 1079, and in The Art of Fugue, BWV 1080. Hofstadter uses some of these works composed by Bach as analogous to the idea of a strange loop. According to Hofstadter, these canons are examples of recursive and self-referential structures present in Bach’s music.

In the piece I am a Strange Loop, I employ the idea of self-referentiality in a somewhat restricted and personal way: The process of referencing occurs between two different works, where one is developed almost entirely through the abstraction and posterior remapping of certain musical parameters coming from a source piece. Therefore, certain preexisting musical information recurs in a new form in a different work. This is the essence of my use of parametrical remapping as a compositional methodology. To a lesser extent, the method involves developing recursive processes that occur within the new piece, where the previously existing musical information sprouts across diverse musical parameters on the new composition and at different levels.
Additionally, an interesting inquiry that emerges with this methodology is connected to the perceptual connection between the preexisting piece and the new one or the degree of presence or absence of the source piece in the new one: Is it possible to create a new piece by remapping information from a preexistent one in a way that these abstract connections between the two become somehow audible? Is there a gray zone where, while we hear a new-to-us composition, some auditory cues are driving our perception to the recollection of a previously heard piece?
Section 1 – Remapping a Profile
As a departure point, I formalized the melodic profile of the theme from Canon No. 2 of the Musical Offering as a linear BPF. This BPF is used as a model for generating new musical representations of it.
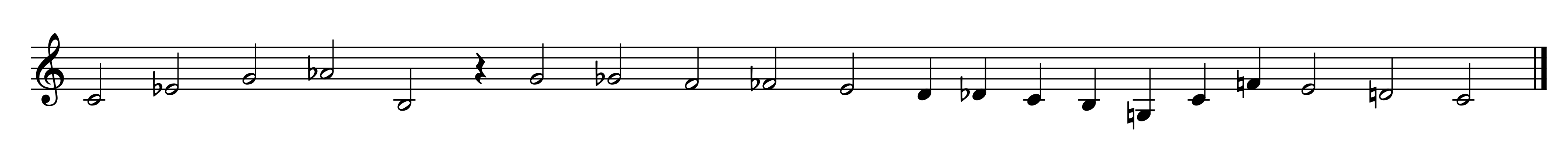
For this piece, I was interested in exploring the musical potential of the subharmonic scale as a source of harmonic material and pitches. Notice that the tonal center of the canon is C minor. For some theorists, the minor mode can be explained as deriving from an inversion of the natural harmonic series. This inversion yields a new scale known as subharmonic. The composer Harry Partch has termed the harmonic processes derived from the subharmonic scale as utonality.*Harry Partch, Genesis of a music: an account of a creative work, its roots and its fulfillments, 2nd, enl. ed. (New York: Da Capo Press, 1974).
The fundamental sub-harmonic note of a minor mode is the 5th note of its root chord –to be very precise, it’s the 5th note of its root chord plus 2 cents. In this case, the C minor mode exists within the undertone series of G8 (+2ct). I use the G8 subharmonic as the source scale for my pitch and harmonic material in the first section of the piece.


To create new melodic material, I used the melodic profile of the original theme as a BPF that I used to map the partials of the undertone series as points in a 2D space (ranging from 4 to 14), where each point represents one of the notes in the new melodic theme. This process is a formal system that can be expressed using a mathematical formulation:
The undertone series is inverted relative to the harmonic series. If we take the fundamental frequency (f0) of our desired undertone series, and if we label the partials as p (with p starting from 4 to 14 as given in your range), the corresponding frequency of the p-th partial is inversely proportional to p:
The pitch y corresponding to each partial can be derived by converting the frequency into MIDI note numbers using the following formula (where 69 is the MIDI note number for A4 (440 Hz):
The melodic profile as a BPF is represented by the set of points (p,y), where y is calculated using the equation below:
Mapping these partials into notes yields an inverted melodic theme to the original. The reason for this is that the direction of the sub-harmonics is inverted from the natural harmonic series, thus higher partials represent lower notes:

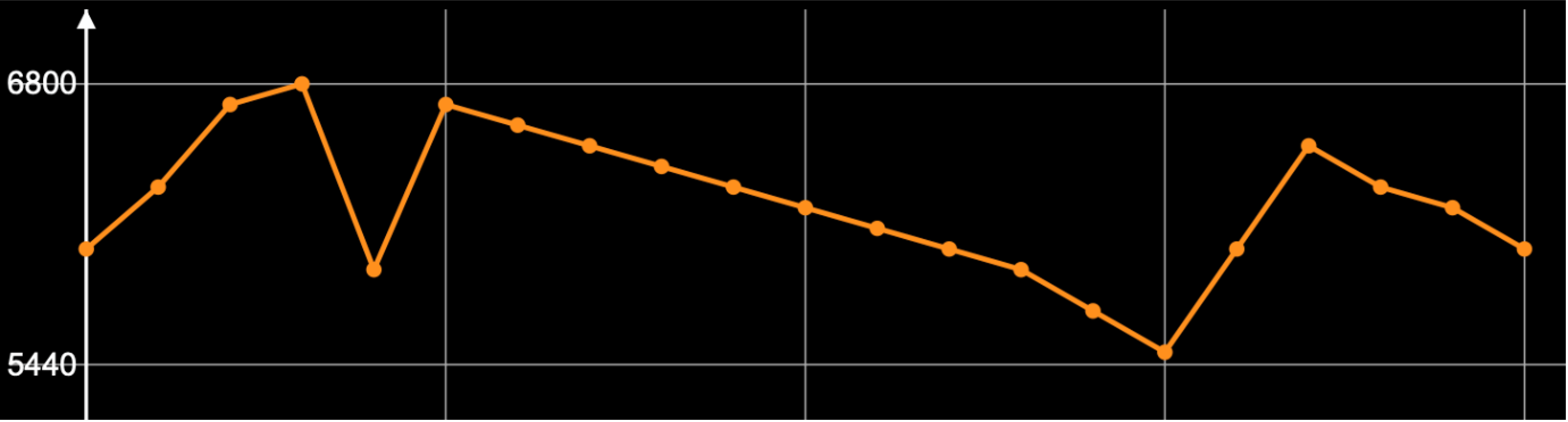
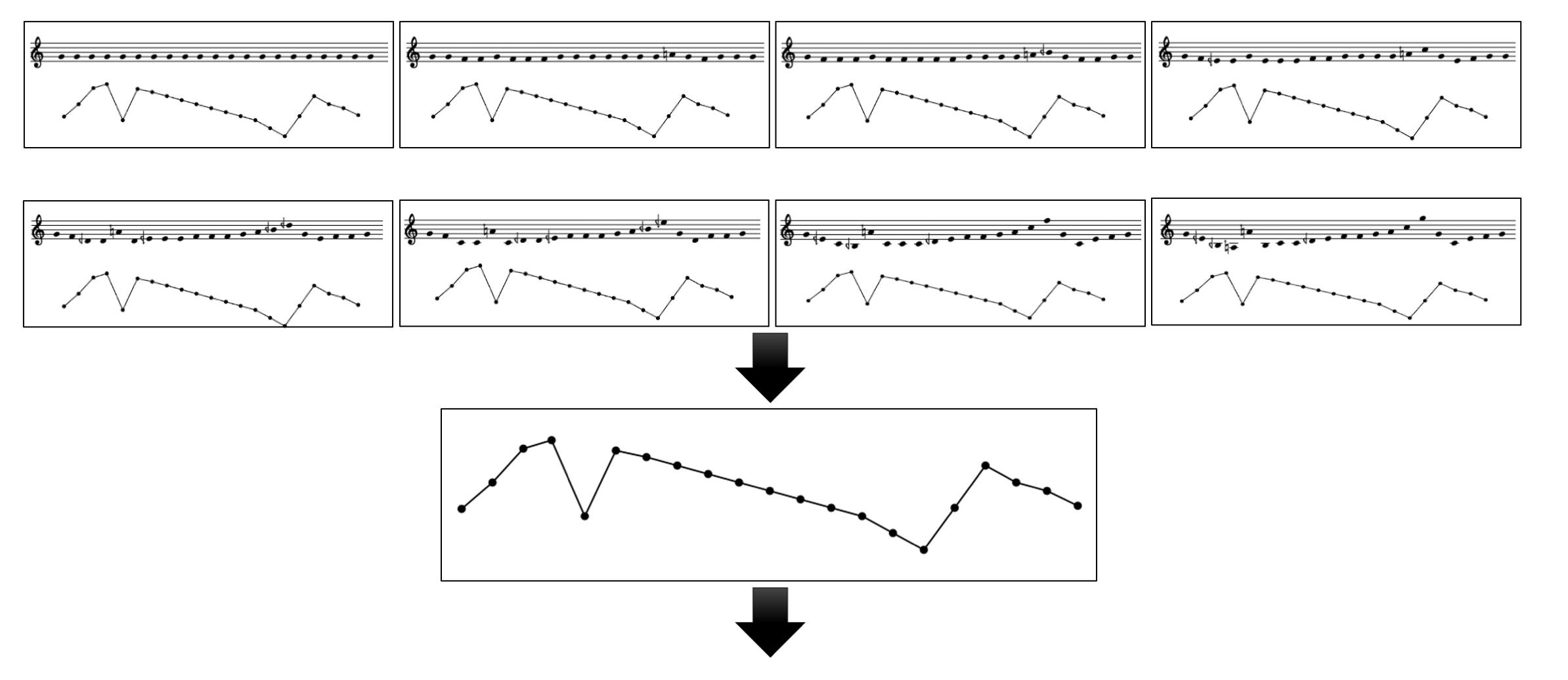
To operate melodic transformation and develop the main theme, in the first section of the piece, this melodic profile is transformed via the use of a perturbation*Initially, I did this using some functions of the external Max package BACH. Later, I realized that some of the functions that I implemented for this process existed previously within the library JBSprofiles in its version for Max, distributed in the external package MOZ’Lib. Further discussion around the idea of profiles and perturbations can be found in Chs. 5 and 6 in Jacopo Baboni Schilingi, La Nuova Pratica: La musique hyper-systémique (Éditions Mix., 2018). process, consisting of progressive intervallic compression over various steps (in this case, eight). When these successive compressions are later organized sequentially, starting from the last step (flat line) to the initial step (original profile), this perceptually relates to a process of expansion. The BPF graph below shows the eight steps of the compression process of the original profile, superimposed on one another. In the score, I present these eight lines sequentially (see the score below), starting from the flat line and ending in the theme in its normal shape.

The noteheads indicate the important or anchoring notes, and the lines indicate regions in between notes. These trajectories have been simplified into a glissando line, which means that the notes in between are not fixed.
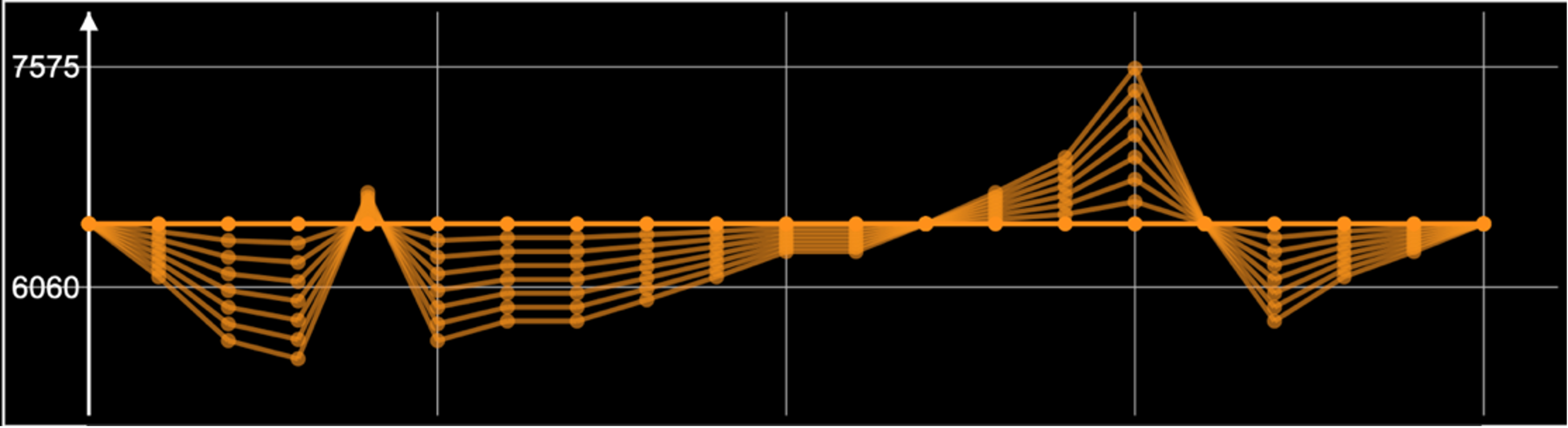
In the domain of durations, I have formalized the melodic profile as a warping temporal factor that alters the chronometric density and durations of events at the level of the individual phrases and at the overall level after the phrases are concatenated. The x-axis represents time, and the y-axis represents the warping factor. Therefore, the higher y values yield a higher chronometric density of events and shorter durations, whereas the lower values yield longer durations and scarce events.

The form of the first section is determined as a loose analogy to the form of Bach’s canon –the source piece. It has two parts of a somewhat equivalent length. In the first part of the first section (m. 1-29), the formal process is derived from the expansion of the original theme, departing from a flat line of pitches and arriving at its original form –the most expanded melodic line– after eight iterations in m. 29 (sop. sax). After this, there is a climatic closing moment that produces a build-up of energy that reaches an abrupt break in m. 49. The second part of the first section develops the inverse idea. Instead of melodic expansion, here, the melodic material is progressively compressed until it gets to a line of repeated notes –a flat line– in m. 70. In addition, the melodic material results from the inversion of the original theme. Therefore, the formal idea for the first section resembles a type of palindrome or cancricans organization –although not canonical, rather, based on the expansion and compression of the thematic material and its inversion.
Multiphonics
The use of multiphonics in the first section follows a certain logic. I utilized a multiphonics database*The database belongs to Quasar Saxophone Quartet, and can be accessed here: https://q-phonics.com/. and applied an algorithm to extract their virtual subharmonic fundamentals. Subsequently, I organized them based on their proximity to the original subharmonic fundamental, from which I derived my pitch material (G8 + 2 cts). From this sorted list, I selected specific multiphonics and incorporated them at various points in the score. Essentially, the sonority of the multiphonics transitions from more consonant to more dissonant in relation to the perceived tonal center –C minor, derived from the G8 subharmonic scale. See the example below:

Outside the system
In the first version of the piece, the thematic material in the first section was developed as a single line that expanded and contracted in the baritone saxophone alone. The other instruments mostly played repeated pitches that expanded and contracted rhythmically, serving as a background. For the second and current version, I decided to re-compose the entire first section and distribute the thematic material across the four saxophones. Additionally, my intention was not for each of these phrases to stand out prominently in the texture; rather, I aimed to create a background from which these melodic figures would emerge and dissolve. My approach was to begin the main phrases on unison notes, which would be held and repeated, allowing the main theme to emerge from them.
An additional layer, prominent throughout the score, features vibratos and varying degrees of airy sounds. This layer was developed during a later compositional stage. One of my heuristic strategies for this layer was to integrate the idea of speed fluctuation present in the rhythmic structure, for instance, having the vibrato evolve from slow to fast and vice versa.

The air sounds, particularly prominent at the beginning of the piece, emerged as a means of connecting material from the improvised sections with earlier material in the piece. Given the essentially distinct sonic results of the improvised section and the written composition, I devised strategies to bridge them, incorporating some posterior adjustments. Ultimately, while the beginning and end of the piece sound quite different, they are sonically connected through the recurring presence of air and air sounds.

Section 2 – Symbolic ring modulation
The second section of the piece comes as the result of applying symbolic ring modulation to the complete canon and transcribing that as the saxophone parts. For this, I computed the RM spectrum using the two voices of the original canon as the carriers and the fundamental note of the subharmonic scale (G) as the modulator. The result is a harmonic spectrum consisting of four sidebands:

This section is also derived from the source piece, still from a relatively abstract process as the calculation of a ring modulation spectrum. However, the notion of presence here somehow takes an unprecedented space since the choral is somehow perceptually relatable to the original Bach’s canon. Furthermore, formally, this section is a literal reproduction of the canon in a different harmonic universe and time-warped: I again used the melodic profile of Bach’s canon theme as a BPF to time-warp the complete choral.
It is worth discussing here how this approach changed in two successive versions of the piece. For the first version, I wrote this section in regular metric notation with a fixed tempo. Even though the sound result should be of gradual accelerandos and rallentandos across large periods, this process yielded a fairly complex rhythmic notation, which made it too complex and somehow misleading for the performers. To explore a better alternative for this, in the second version, I changed this notation into fixed rhythmic values along with gradually speeding up/slowing down tempo marks. Since the ensemble moves in homophony, there are no issues of multi-temporality, as in the first section, where every phrase is warped differently and does not match with the other parts of the ensemble. In this case, it is necessary to adopt a general tempo and write each part in relation and proportion to it. The ring-modulation chorale was re-notated completely from the first to the second version. See below:


Reeds duo part
The reeds duo consists of an accordion and an organetto portativo, which appear in the second section of the piece. Initially, I envisioned them as emerging from the ring-modulation chorale, where they gradually prolong certain pitches before becoming more active and independent. To achieve this, the tuning of the organetto is adjusted to align with the microtonality present in the saxophone parts. The accordion, on the other hand, remains more subdued at first, acting as a subtle background that slowly becomes more prominent towards the end of the section. The two instruments become more prominent in the final improvised section.

Section 3 – Improvisation
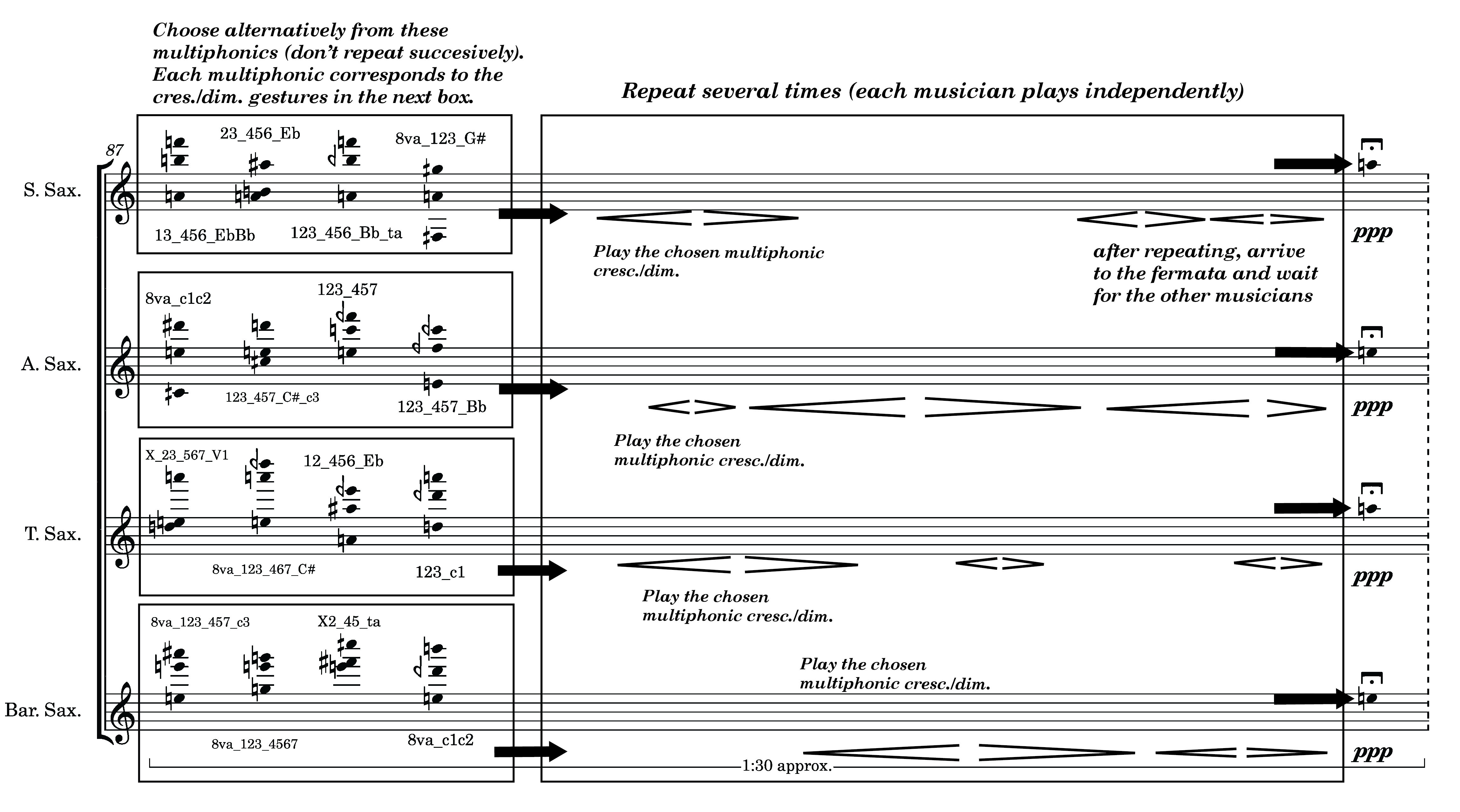
The final section of the piece consists of an improvisation part that follows some guidelines. Overall, in this section, the note G (fundamental pitch from the subharmonic scale) stands out. In the first part of it, the saxophones must choose from a subset of multiphonics, all of them containing the pitch G within their component notes. This gives the overall sonority a relatively homogenous sound. Gradually, the material expands to include vibrato and flutter-tongue sounds, ultimately fading into air sounds, connecting back with this material as it was presented in the first part of the piece.
Here, the reeds duo becomes responsive to what the saxophone quartet does without further indications of actions or techniques. The saxophones’ part evolves gradually; multiphonic sounds become pitched sounds (note G) with vibrato and flutter-tongue, and finally, these morph into air sounds. The piece fades into air and noise.

Electronics
The electronics appear in the improvised section and are primarily generated from brain readings of one of the performers using an fNIRS helmet. These readings are live-mapped into digital signal processes within Ableton Live 12 through a Max4Live device that I developed in collaboration with Ryan McCardle: fNIRS_to_Live, which I will discuss more on it in the section ‘Contributions.’
For the current performance, the selected processes included resonant filters, panning, delay, reverb, and a granulator, with parameters such as delay times, the number of resonators, and grain size and density. While fNIRS_to_Live allows for mapping all forty-two stream channels coming from the fNIRS helmet into Ableton Live parameters, I limited the mapping to sixteen channels for this performance. Each of the sixteen channels affects one parameter individually. See the video below:
The idea of a strange loop is also connected to the electronic part, as brain readings –mainly taken from the auditory and motor cortex– are initially triggered by the auditory stimulation from the sounding music. During the performance, the performers should respond to these improvised sounds. These responses, in turn, create new sounds, which influence the brain readings, forming a recursive musical strange loop. The result of this process is a subtle layer of electronic sounds and processes that seamlessly blend into the overall texture, adding an additional dimension: a kind of aura.



