The Cognitivist Paradigm

Cognitivism

In cognitive sciences, the theoretical approach that views the human mind mainly as a system that primarily manipulates and processes symbols and symbolic representations is known as cognitivism. From this perspective, cognition is seen as essentially being computation: the mind is viewed as a machine* The idea of the machine comes from the Turing machine. It was first theorized by Alan Turing in 1936, and it describes a theoretical computational model consisting of an infinite tape and a finite set of rules that dictate how symbols are read, written, and manipulated to perform computational processes. Moreover, Turing machines are considered to be one of the foundational models of computability. In Turing, "On computable numbers, with an application to the Entscheidungsproblem." that processes symbols, with thoughts organized into symbolic systems that can be articulated in a structured, logical manner.

The ideas of cognitivism initially emerged in the work of the computer scientists Allen Newell and Herbert Simon and the philosophers Hilary Putnam, Gilbert Harman, and Jerry Fodor. In his book Modularity of the Mind, Fodor proposes that having a mind entails that we are equipped with a sophisticated assembly of numerous computers, each dedicated to a distinct mental function such as perception, memory, language processing, decision-making, and motor control. These computers are interconnected within a complex “computational architecture,” where the output of one subsystem serves as the input of another.* Jerry A. Fodor, The modularity of mind (MIT Press, 1983).

Fodor also discusses an important concept, which is related to the modularity and non-modularity of cognitive systems. Fodor argues that some of our cognitive systems are encapsulated, meaning they operate independently of each other and are not influenced by general knowledge or other cognitive processes. This encapsulation allows for efficient and rapid processing within specific domains. Fodor also acknowledges the existence of non-modular, central systems that integrate information from various modules to perform higher-level cognitive tasks like decision-making and problem-solving.

Symbolic AI

The first scientists working with AI became fascinated by cognitivist theories, and in fact, the first developments in AI were based on implementations of logical systems of learning and decisions. Scientists like John McCarthy and Marving Minsky were convinced that the human mind was a huge computer, and creating systems that imitate the human mind would eventually lead to the development of an intelligent system.* The first conference that brought together top researchers from various fields for an open-ended discussion on AI was the Dartmouth Summer Research Project on Artificial Intelligence (DSRPAI) hosted by John McCarthy and Marvin Minsky in 1956.

Symbolic AI is an approach that involves representing knowledge using symbols and manipulating those symbols to perform reasoning and problem-solving tasks. In symbolic AI, the focus is on building systems that can reason about abstract concepts, use them to solve problems, and eventually transfer these concepts into different knowledge domains, including those involved in creativity.

Some theorists have linked human creativity to a computational process rooted in the symbolic processing and organization of information. In music composition, for example, we might consider creativity as guided by rules that shape musical form, material, technique, and style. Approaching the process of composing from a cognitivist perspective has guided my exploration of the first ‘labyrinth’ in the piece Versificator – Render 3. However, a natural question arises: is creativity solely about logical formulations, rules, and computational algorithms?

The Question of Computability in Music Composition

The notion of computability in composition dates back to the 1950s when some composers began drawing analogies between creative methods and computational processes. The composer Petr Haas notes that the use of algorithm-like* An algorithm is a set of step-by-step instructions designed to perform a specific task or solve a particular problem. In Thomas H. Cormen et al., Introduction to Algorithms, Third Edition, 3rd ed. (Cambridge: Cambridge: MIT Press, 2009). methods in composition dates back to the complex evolution of polyphonic music and the advent of musical notation systems.* Petr Haas, "The language of the assistant and the language of the creator: selected aspects of computer assisted composition," Musicologica Brunensia 52, no. 2 (2017), https://doi.org/10.5817/MB2017-2-12. Over the centuries, compositional methods gradually shifted toward rule-based processes, which led composers toward desired musical outcomes.

As an example, it is possible to observe the works of historical figures such as Guillaume de Machaut and Phillipe de Vitry as these demonstrate this early propensity for isorhythmic composition, even when this method sometimes would go to the detriment of the text’s congruence with the music. Isorhythm (trad. From Greek: “the same rhythm”) is a compositional technique that emerged around the 13th century. It consists of iteratively pairing together single rhythmic and melodic independent units, that function independently from one another.

In the opening of the “Kyrie I” from the Messe de Notre Dame by Guillaume de Machaut (1300-1377), there is a twenty-eight-note color arranged into seven talea. Each talea consists of four note durations. After seven repetitions of the talea, the twenty-eight notes of the color reappear from the beginning:

Modern notation transcription of the isorhythmic tenor line from the opening “Kyrie” of Guillaume de Machaut’s Messe de Nostre Dame (c. 1360). Here, a color consisting of twenty-eight pitches is structured with a talea of four rhythmic values, repeated seven times (28 ÷ 4 = 7).*Guido Magnano at Italian Wikipedia. - Transferred from it.wikipedia to Commons., Public Domain, https://commons.wikimedia.org/w/index.php?curid=1944847

An isorhythmic process can be described as the manipulation of two lists: one, an ordered collection of duration values –a talea, and the other, an ordered collection of pitch values –a color. Each list is looped separately and in parallel. For each cycle, the elements from both lists are paired consecutively, with one element from talea paired with one element from color. If one list is shorter than the other, it will run out of elements before the longer list finishes, at which point the shorter list is looped back to the beginning. Using lists of different lengths is a common feature of this technique. The overlapping of lists prevents them from realigning at the end of each loop. As a result, with each repeat, talea and color will coincide at different positions in the lists before all combinations are completed. As an example, let us consider the following talea (A B C) and color (W X Y Z). Below can be seen each iteration of the loop:

• Iteration 1: ((A W) (B X) (C Y))
• Iteration 2: ((A Z) (B W) (C X))
• Iteration 3: ((A Y) (B Z) (C W))
• Iteration 4: ((A X) (B Y) (C Z))
• Iteration 5: ((A W) (B X) (C Y)) — The sequence has now returned to the starting configuration.

This simple isorhythmic process can be expressed as computer code. Below, in Lisp:* Lisp is a family of programming languages designed by John McCarthy in 1958. It is characterized by its fully parenthesized syntax and nested list-based data structures, making it particularly well-suited for processing symbolic information and creating recursive functions. Lisp became foundational in the development of artificial intelligence during the 1960s and 1970s. For a long time, Lisp became the norm for musical programming and computer-assisted composition, in part, due to the similarities between Lisp’s lists, which can closely represent the complexity of symbolic musical representation as scores.

  (progn  ; Group multiple expressions to evaluate them sequentially.
    (setq talea '(A B C))  ; Set the variable `talea` to a list of symbols: '(A B C).
    (setq color '(W X Y Z))  ; Set the variable `color` to a list of symbols: '(W X Y Z).
  
    (defun pair-talea-color (talea color)  ; Define a function named `pair-talea-color` that takes two arguments: `talea` and `color`.
    (let* ((talea-length (length talea))  ; Calculate the length of the `talea` list and store it in `talea-length`.
           (color-length (length color))  ; Calculate the length of the `color` list and store it in `color-length`.
           (cycle-length (lcm talea-length color-length)))  ; Compute the least common multiple (LCM) of `talea-length` and `color-length`, storing it in `cycle-length`.
    (loop for i from 0 below cycle-length  ; Loop from 0 up to below `cycle-length`.
          collect (list (nth (mod i talea-length) talea)  ; Get the `i`-th element of `talea`, cycling using `(mod i talea-length)`, and pair it...
                        (nth (mod i color-length) color)))))  ; ...with the `i`-th element of `color`, cycling using `(mod i color-length)`.

  (pair-talea-color talea color))  ; Call the `pair-talea-color` function with the `talea` and `color` lists and return the resulting list.

  ;; result: '((A W) (B X) (C Y) (A Z) (B W) (C X) (A Y) (B Z) (C W) (A X) (B Y) (C Z))

Haas further refers to Johann Joseph Fux’s influential treatise Gradus ad Parnassum (1725) as a foundational rule-based system, particularly for mastering counterpoint. According to Haas, the more precise the formulation of these rules, the “stricter” the counterpoint or method, the easier it becomes to translate into machine language.* Haas, "The language of the assistant and the language of the creator: selected aspects of computer assisted composition," 122. This is exemplified by the Illiac Suite (1958), the first recognized piece created using a computer, which bases an entire movement on Fux’s counterpoint principles, by translating complex polyphonic rules into computational logic.

Other composers, such as Iannis Xenakis and Gottfried König, were also pioneers in this field. Their vision and understanding of human creative processes in music composition acted as catalysts for employing computers in composition, viewing them as somewhat analogous to a composer’s creative process. With their ability to provide greater processing power, speed, and advanced search methods for solving specific musical problems, computers were seen as valuable tools for advancing research in composition. Unlike Hiller and Isaacson’s approach, however, these composers aimed to develop a logic of musical composition that transcended specific stylistic or historical methodologies.

“Naturally, one does not program known rules of composition but also tries to find out whether events not yet expressed in the form of rules are feasible. The computer thus has a stimulating effect on research in composition theory.”

Xenakis metaphorically describes his creative process involving the use of electronic computers as piloting a spaceship:

“Freed from tedious calculations, the composer can devote himself to the general problems posed by the new musical form and explore the corners in this way while modifying the values of the input data. (…) With the help of electronic computers, the composer becomes a kind of pilot: press buttons, enter coordinates, and supervise the controls of a cosmic ship that navigates in the space of sound through sonic constellations and galaxies that before could only glimpse as a distant dream. He now can explore them easily, sitting on a sofa.”

Eventually and over time, computers came to be seen as a valuable tool that could contribute to the advancement of musical form and expression and more composers accepted them as a valid means for composing, even when this involved significant degrees of automation and little or no direct human intervention in the process.

Musical search spaces

In Western art music, especially, several composers have referred to composing as a process of exploration of a search space. For example, the notion of basic space, proposed by Fred Lerdahl,* F. Lerdahl, Composition and Cognition: Reflections on Contemporary Music and the Musical Mind (University of California Press, 2019). or the idea of musical search spaces, proposed by Lejaren Hiller* Lejaren A. Hiller and Leonard M. Isaacson, Experimental Music: Composition with an Electronic Computer, (New York: McGraw-Hill Book Company, 1959). even earlier, around the decade of 1950.

This poses interesting questions: Can we understand the process of composing as a structured exploration within a musical search space? If so, what does this exploration involve, and what kinds of choices define this process? Is the search space shaped by pre-existing cultural and stylistic conventions, or does it remain open-ended, shaped solely by the composer’s intuition and formal innovations? Additionally, how do constraints, such as rules of rhythmic, melodic, or harmonic movement, and even instrumental/vocal limitations, among others, impact the scope and boundaries of the search space, and to what extent do they direct the composer’s exploration of it?

Constraint algorithms

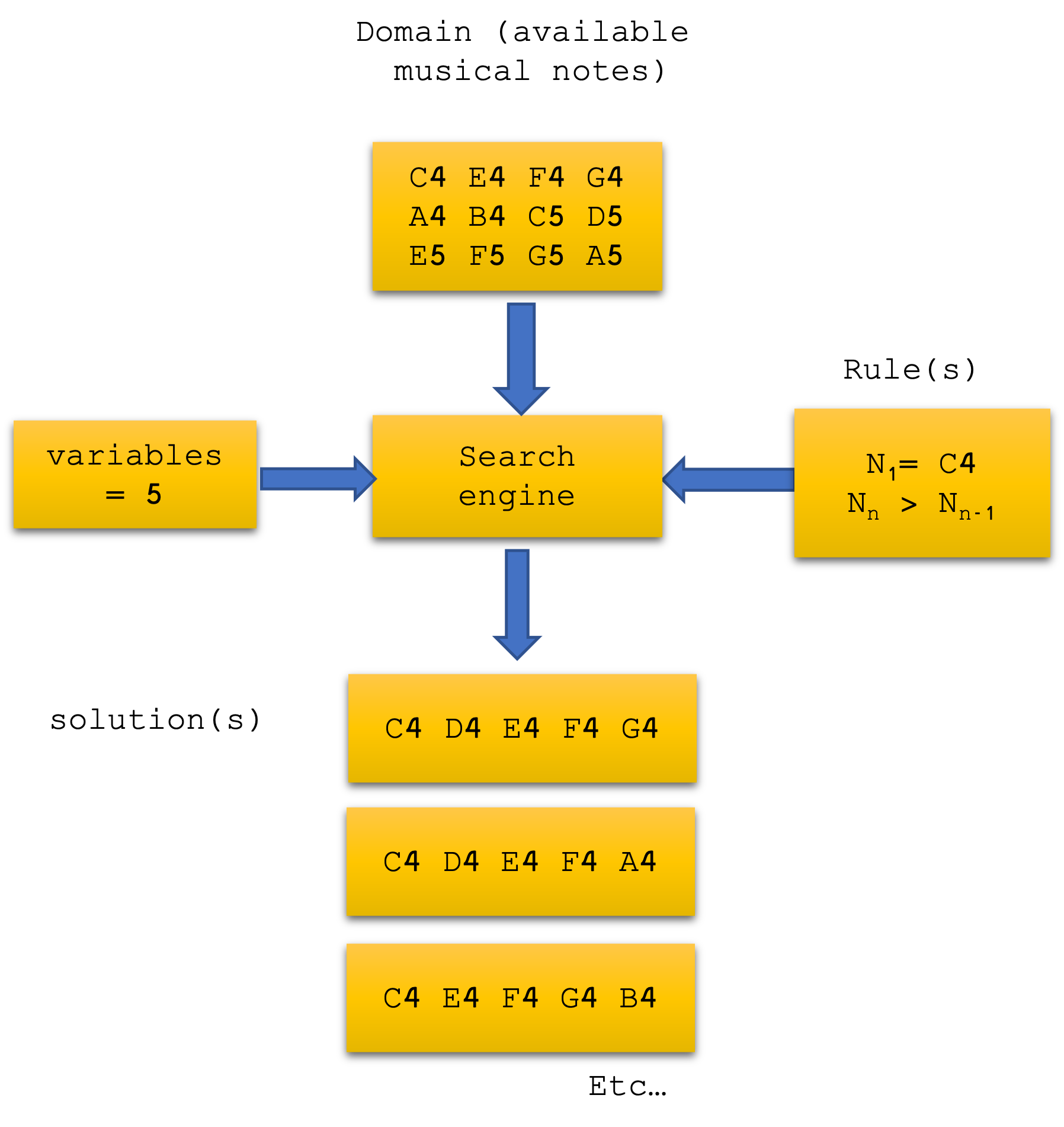
A constraint algorithm is a computational method that searches for values for a set of variables that satisfy a set of constraints, ensuring that all conditions or rules are met. In the field of music composition, particularly in computer-assisted composition, constraint algorithms have a very long history.

The primary components of a constraint satisfaction algorithm in music composition include:

• Variables: These are the elements that need to be assigned a value. In its application to music composition, for example, each variable could be a specific note in a melody.
• Domains: Each variable has a domain, which is the set of possible values that the variable can take. If we take melody, for instance, the domain for melodic variables could be constrained by certain notes, depending on the melodic or harmonic context at different points in time.
• Constraints: These are rules that restrict the values the variables can take. If we think of a melody, then we might want to allow/prevent certain notes from following others or to prohibit certain notes in certain moments of the melody, for example, at the beginning, end, strong or weak beats, or only allow for specific pitches considering the range of the instrument, etc.

The way that constraint algorithms work is rather simple. One determines the variables and their domains –consisting of a set of musical elements that those variables can take– and rules for a particular musical organization for these elements, and the algorithm sorts the musical elements by enforcing this rule or set of rules by iterating through every possible combination of elements until it finds a solution or multiple solutions, or until it finds none. The rules are usually expressed as logical statements, and each candidate solution will be evaluated as true or false. Those evaluated as true are accepted and returned to the user, and those evaluated as false are rejected.

A simple example of how a constraint satisfaction algorithm works. Here, the variables are five consecutive melodic notes. The domain is a set of 12 notes (here expressed as pitch class + octave). Each variable can take one of those 12 values. two rules are defined; the first one states that the first note should be C4, and the second rule states that each note should be higher than its predecessor. The solutions that satisfy these rules are several. The engine thus might return as many as desired –maybe only one- or as many as exist.

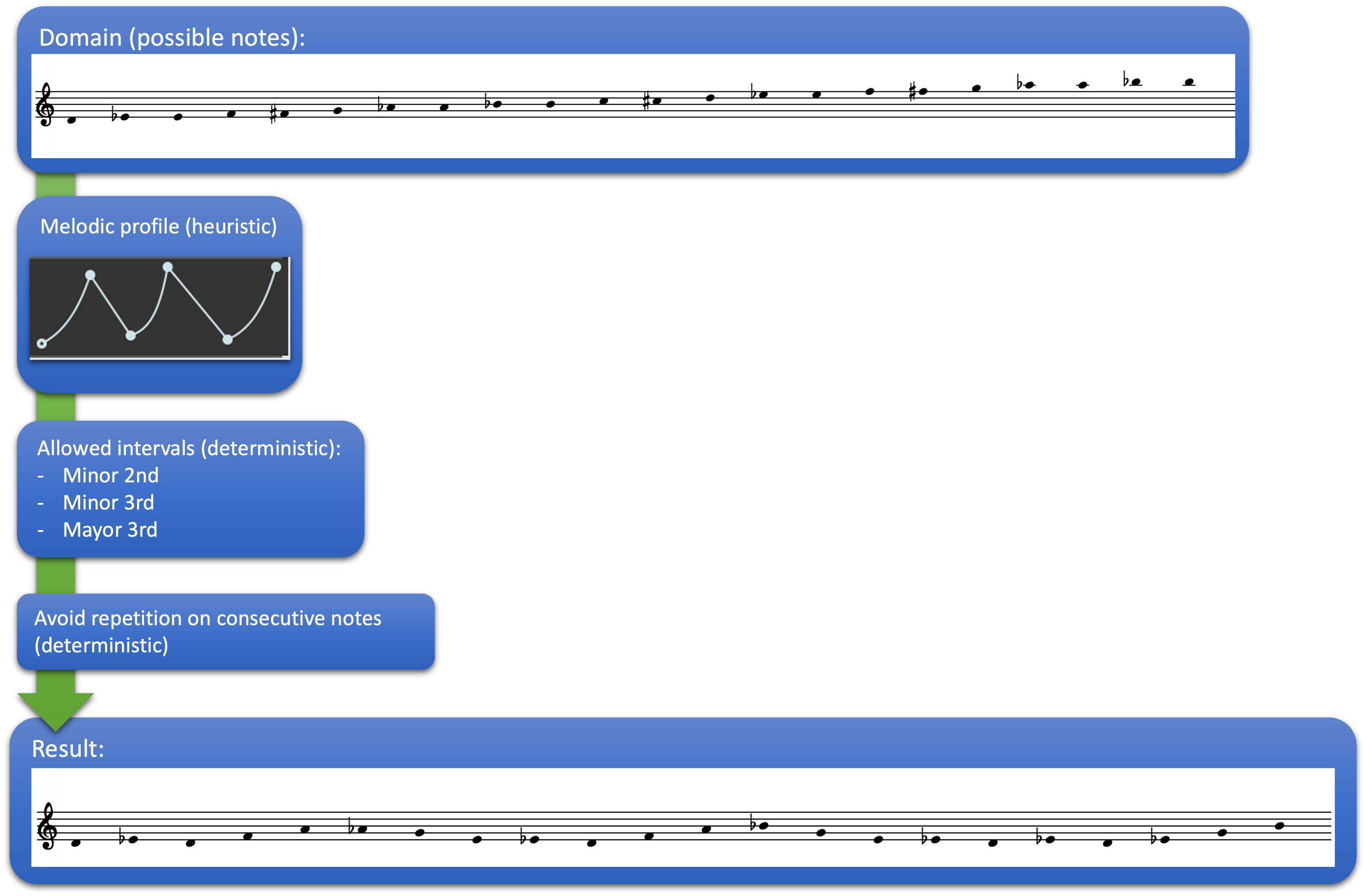
It is also possible to weigh certain choices of the algorithm instead of ruling them out. For this, other types of rules are more flexible, known as heuristic rules. Heuristic rules allow for solutions that do not totally fulfill the rule. Instead, each candidate solution is assigned a weight expressed as a numeric value. The higher the weight, the better the candidate solution fulfills the rule. Heuristic rules are generally used for musical parameters that allow for certain flexibility. As an example, consider a melodic profile: it is determined by an overall contour, but the notes are not necessarily fixed, and several options are possible for each variable as long as the contour remains.* A CAC library focused on profiles is JBS-profiles, developed by Jacopo Baboni-Schillingi. Its documentation is available at: http://baboni-schilingi.com/images/Reseacrh-files/jbs-profile.pdf Additionally, the Max external package CAGE includes functions for compositional operations with profiles. Max, a musical programming language in a patching environment, can be accessed at https://cycling74.com/. CAGE can be downloaded directly from the Max package manager or from https://bachproject.net/. Throughout this project, I have used both tools in different situations, but their functionalities are almost analogous.

Example of a melodic contour used as a heuristic rule. Here, a given profile is applied as a heuristic rule, and two chained true-false rules (the technical term is deterministic) determine allowed intervals and repetitions.*Source: Örjan Sandred, The musical fundamentals of computer assisted composition (Winnipeg MB: Audiospective Media, 2017).

Cluster-Engine

So far, my description around constraint algorithms seems to paint them as a brute-force tool closer to a calculator than anything musical. However, that is not the whole story. Some constraint algorithms are quite advanced in their architecture and designed to resemble closely the musical compositional situation. An example of this is the constraint solver Cluster-Engine (CE).* Cluster-Engine was developed by Örjan Sandred. See Örjan Sandred, "Constraint-Solving Systems in Music Creation," in Handbook of Artificial Intelligence for Music: Foundations, Advanced Approaches, and Developments for Creativity, ed. Eduardo Reck Miranda, 1st Edition 2021 ed. (Springer International Publishing AG, 2021).

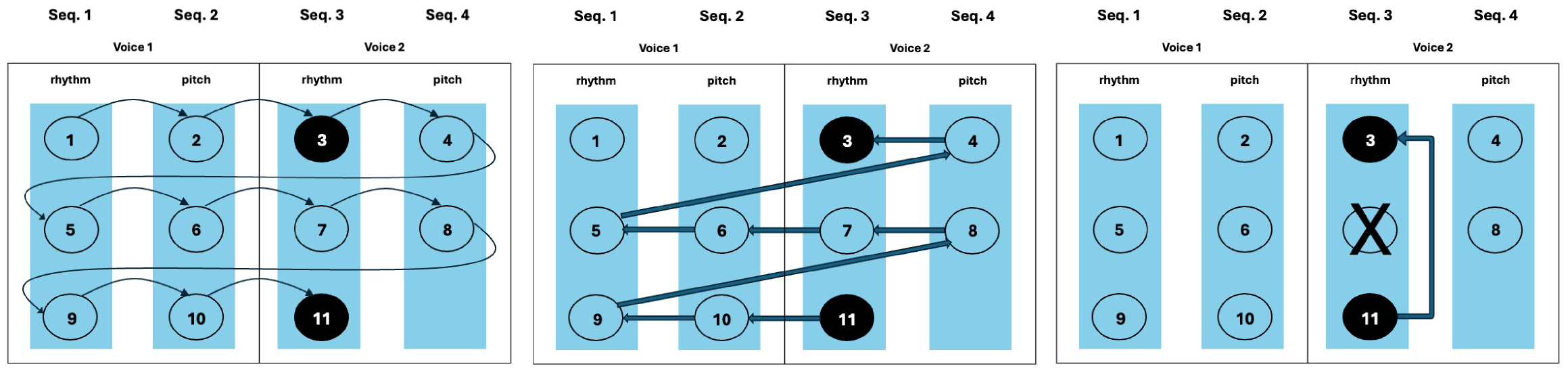
CE is a Lisp-based constraint solver designed to address complex musical problems by integrating rhythm, pitch, and meter across multiple voices within a unified sequential search process. Initially developed as a library for the composition environment PWGL, CE has since been ported to Max* Max 8 is a musical programming language in the form of a patching environment. It is available at https://cycling74.com and is now distributed as part of the external package MOZ’Lib.* https://github.com/JulienVincenot/MOZLib A key feature of MOZ’Lib is its ability to execute Lisp code directly within the Max environment, facilitating the use of CE and other Lisp-based functionalities in Max.* Julien Vincenot, "LISP in Max: Exploratory Computer-Aided Composition in Real-Time," ICMC 2017 proceedings (Shanghai, 2017), http://hdl.handle.net/2027/spo.bbp2372.2017.012.

CE enables the codification of musical rules allowing for reciprocal influence of harmony, rhythm, beat structure, or melodic movement across multiple voices. It supports the use of domains encompassing individual pitches or groups (melodic motifs), intervals or interval groups (intervallic motifs), and individual durations or groups (rhythmic motifs). CE represents each musical voice using two distinct sequences: one for durations and another for pitches. For a two-voice score, this results in four sequences. Additionally, a global sequence is used to represent metric structure (time signature and subdivision). As a result, solving constraints for two voices would require five engines in total.

Unlike traditional constraint systems, CE splits a problem among various search engines working in parallel, sharing partial solutions. Additionally, they have the capacity to prompt one another to backtrack during the search process. The advantages of dividing the problem across multiple engines become apparent when logical conflicts arise, and backtracking becomes necessary. CE can identify which variable caused a given conflict, enabling a direct backjump to that position to bypass intermediate steps. While respecting the variable visitation order, backtracking can occur within any independent sequence, leaving others undisturbed. This significant improves the process’ efficiency.

a) Example of CE’s normal search process; b) Example of the sequential backtracking method used in other constraint solvers. In the event of a conflict between two variables in a two-voice musical scenario (e.g., variables 3 and 11 in the rhythm sequence for voice 2), all intermediate values are erased; c) CE’s backtracking method employs backjumping, which directly targets the source of the conflict. Once variable 3 is reassigned, only variable 7 requires recalculation.*Sandred, "Constraint-Solving Systems in Music Creation." (2021)

Some relevant contemporary composers that use constraint algorithms for composing are Mikael Laurson, Jacopo Baboni Schillingi,* J. B. Schillingi is the creator of the CAC library JBSconstraints, an integral approach for applying constraints in music composition in different musical domains, such as pitch, intervals, distance, structure, etc. Magnus Lindberg,* A relevant musical composition that resonates with me is Engine (1996) by Magnus Lindberg. The title is inspired by the computational realm, specifically tied to the use of the PatchWork environment and its constraint engines (PWConstraints). In this context, the engine functions as a generative mechanism for musical material, operating under a set of predefined rules determined by the composer. Johannes Kretz,* Johannes Kretz has composed several pieces using constraint algorithms, for example, the piece ‘Second Horizon’ for piano and orchestra. For a description of the compositional process, see Johannes Kretz, "Navigation of structured material in second horizon for piano and orchestra," The OM composer’s book 1 (2006). Julien Vincenot, and Torsten Anders,* Torsten Anders is the creator of the library Cluster-Rules, an extension of the music constraint solver Cluster-Engine The source code can be found here: https://github.com/tanders/cluster-rules. among others. Many great musical pieces have been composed relying on this methodology.* For a detailed survey, see Torsten Anders, "Compositions Created with Constraint Programming," in The Oxford Handbook of Algorithmic Music, ed. Roger T. Dean and Alex McLean (Oxford University Press, 2018).

An example of the compositional use of constraint algorithms is the piece Memorie de l’eau (2015) by Julien Vincenot. In it, the musical material consists of virtuosic passages inspired mainly by improvisation in free jazz. To generate the musical material, the composer determined a complex search space that comprised transposable melodic motifs and chords, considering the efficient and idiomatic possibilities for the accordion. To generate musical structures using that search space, the composer applied two categories of rules involving the use of two voices (one for each manual of the accordion). The first category is related to idiomatic performance. Here is an example of some rules employed for this purpose:

• Restrict the allowed register for each hand.
• Avoid local repetitions as much as possible (heuristic rule).
• For rhythmic values faster than an eighth note, allow the pitch engine only to select a chord if it is repeated one or two times with an identical rhythm (the equivalent of a “bellows shake” for the accordion); otherwise, choose a single note.

The second set of rules is dedicated mostly to rhythm and controls some aspects of the pitch engines relative to the rhythmic context. As an example:

• Forbid consecutive silences.
• Forbid the nth consecutive thirty-second note.
• Force rhythmic hierarchy between voices (the right hand must follow the left hand’s basic grid and add details on top of it).
• In some contexts, if the current rhythmic value of the right hand is slower than a sixteenth note, then force the corresponding pitch engine to choose a chord.

Excerpt from the introduction to Memoire de l’eau (2015) for accordion and live electronics.* For a complete description of the piece and the composer’s methodology see Julien Vincenot, "On 'slow' computer-aided composition," in OpenMusic Composer's Book Vol. 3, Éditions Delatour - IRCAM Centre Pompidou (2016).